It is common to integrate with decentralized exchanges (DEX) while building DeFi products. Curve is the most preferred choice when it comes to stable coins because of low slippage. However, to integrate with such protocols, one needs to clearly understand its automated market maker (AMM) design. Curve’s stableswap AMM algorithm is more complex and calculation-heavy than Uniswap’s constant product AMM.
In this post, I have explained the maths behind the stableswap invariant, the method used to solve it, and how it is used in the protocol while swapping tokens or finding other parameters.
StableSwap Invariant
An invariant is an equation that defines the relationship between balances of pool tokens and pool parameters. The AMM design makes sure that this relationship is strictly followed before and after each trade. Examples of invariants are
- Constant sum or linear invariant
$$\sum x_i = const$$
- Constant product invariant
$$\prod x_i = const$$
Stableswap invariant is a combination of the above two and offers very low price slippage than Uniswap for stable coin pools. It is given by
$$\begin{equation} An^n\sum x_i + D = DAn^n + \frac{D^{n+1}}{n^n\prod x_i} \end{equation}$$
where $x_i$ represents the balance of $i^{th}$ token in the pool, $D = \sum x_i$ is the total amount of tokens when they have an equal price i.e. at equilibrium when all tokens have equal balance, $A$ is the amplification coefficient and $n$ is the number of tokens in the pool. To know more, check out the derivation of the above equation in the Curve whitepaper.
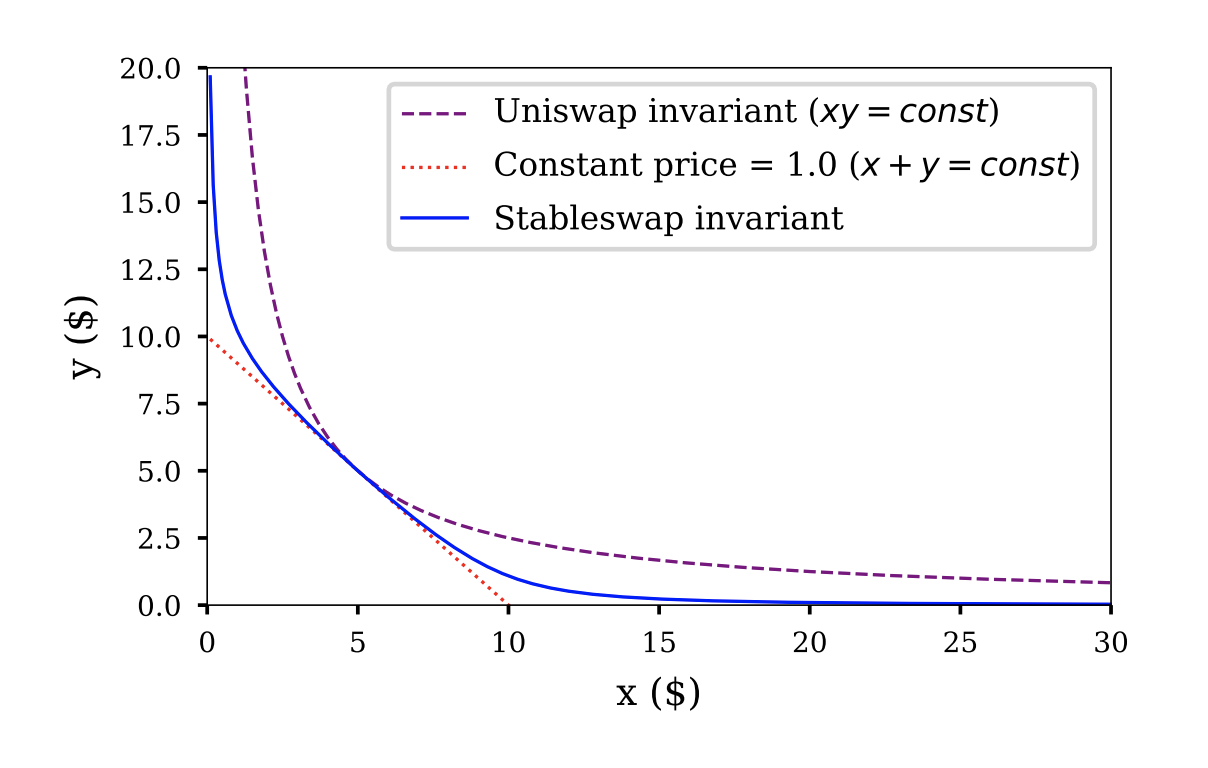
Figure 1: Comparison of constant product, constant sum, and stableswap invariant
As it can be seen in Figure 1, the stableswap invariant is a combination of the constant sum and constant product invariant. Check out this notebook to see the impact of different parameters on the stableswap invariant curve.
Let’s write $An^n$ as $Ann$ as in the contract code then the above equation can be rewritten as
$$\begin{align} \label{eqn:stableswap} Ann\sum x_i + D = DAnn + \frac{D^{n+1}}{n^n\prod x_i} \end{align}$$
This is the equation that Curve’s AMM follows for stable coin pools. This basically means that if a trader wants to swap token $x_i$ (input token) with token $x_j$ (output token), to get the amount to token $x_j$ that needs to be transferred to the trader, equation $\ref{eqn:stableswap}$ need to be solved for $x_j$ assuming all other parameters are constant and known. Newton’s method is used to solve the above equation numerically.
Newton’s Method
Newton’s Method, also known as Newton Raphson Method, is an iterative process that can approximate solutions to an equation with incredible accuracy. It’s a method to approximate numerical solutions (i.e., x-intercepts, zeros, or roots) to equations that are too hard for us to solve by hand. To find the roots of the equation $f(x)=0$, the following equation is iterated until a sufficiently precise value is reached.
$$\begin{equation} x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)} \end{equation}$$
where $f(x_n)$ is continuously differentiable in the vicinity of the root. Check out the simulation of Newton’s method here to get a feel of it.
Swapping Tokens
Coming back to the StableSwap equation, let’s look at how it is used in the Curve protocol. I have taken 3pool (DAI/USDC/USDT ) as an example.
Let’s say the trader wants to know the amount DAI will they receive for depositing $dx$ amount of USDC. In this case, the input token $i$ is USDC, and the output token $j$ is DAI. The updated amount of USDC in the pool can be calculated as $x = x_i + dx$ where, $x_i$ is the current balance of USDC. Since the token amounts always need to follow the StableSwap invariant, updated DAI amount ($y = x_j$) in the pool can be calculated by numerically solving equation $\ref{eqn:stableswap}$ for $y$ and with the amount of USDC equal to $x$. But first, let’s rearrange the equation $\ref{eqn:stableswap}$ which forms a polynomial equation of degree $2$ in $y$ and can be simplified as
$$\begin{equation} f(y) = y^2 + (b-D)y - c = 0 \end{equation}$$
where,
$$b = S + \frac{D}{Ann},~~~~~c=\frac{D^{n+1}}{n^nPAnn}, ~~~~~ S= \sum_{i\not=j}^{n}x_i, ~~~~~ and ~~~~~ P = \prod_{i\not=j}^{n}x_i$$
The root of the above equation can be calculated using Newton’s method by iterating the below equation until convergence.
$$\begin{equation} \label{eqn:getYIteration} y_{n+1} = y_n - \frac{y_n^2+(b-D)y-c}{2y_n +b-D} = \frac{y_n^2+c}{2y_n+b-D} \end{equation}$$
Finally, the amount of token $j$ to be received by the trader can be calculated as $dy = y_{initial} - y_{final}$, where $y_{initial}$ is the balance of token $j$ before the trade and $y_{final}$ is the updated balance calculated from equation $\ref{eqn:getYIteration}$. Check out the implementation of the above algorithm in the get_y(i,j,x,xp) function of 3poolSwap contract. The variable naming is consistent with the code.
Parameter D
The value of parameter $D$ is calculated by solving equation $\ref{eqn:stableswap}$ for $D$, given all other parameters are constant. The function $f(D)$, which a polynomial function of degree $n+1$ can be represented as
$$\begin{equation} f(D) = \frac{D^{n+1}}{n^n\prod x_i} + (Ann -1)D - AnnS = 0 \end{equation}$$
where $S=\sum x_i$. The derivative of above function is $f'(D) = (n+1)D_P/D + (Ann-1)$, where $D_P = \frac{D^{n+1}}{n^n\prod x_i}$. Therefore, the root of $f(D) =0$ can be calculated using newtons formula by iterating below equation until convergence.
$$\begin{equation} D_{n+1} = D_n - \frac{f(D_n)}{f'(D_n)} = \frac{(AnnS+nD_P)D_n}{(Ann-1)D_n+(n+1)D_P} \end{equation}$$
This is implemented in the get_D(xp, amp) function of the 3poolSwap contract and is called before performing any swap.
Next Up
Stableswap invariant works fantastically for stable coin pools and has lower price slippage and higher APR compared to existing AMMs like the constant product. However, it cannot be used as it is for non-stable coin pools. For that, a little tweak is required in the stableswap invariant. Curve has introduced CurveCrypto invariant which is encouraged from stableswap invariant and can be used for non-stable coin pools like the tricrypto2 pool. In the next post, I will be explaining the CurveCrypto invariant and how is used as AMM in the tricrypto2 pool.